学科测评首页

三角形全等（截长补短）（人教版）（专题）1754556017369

满分100分    答题时间45分钟

已经有0位用户完成了练习

单选题(本大题共小题， 共分)

1.(本小题14分) 已知：如图，在△ABC中，∠1=∠2，AC=AB+BD．
求证：∠ABC=2∠C．

先在图上走通思路后再填写空格内容：
①已知AC=AB+BD，是线段的和差倍分，考虑         ，这里采用截长来证明；
②结合条件∠1=∠2，考虑                             （辅助线），然后证全等，理由是       ，由全等的性质得         ，为接下来证明准备条件；
③由已证的全等和已知AC=AB+BD，得        ，过点E作EF⊥BC，垂足为点F，用HL可证△EDF≌△ECF，所以∠EDF=∠C，从而得∠AED=2∠C，即∠ABC=2∠C．
以上空缺处依次所填最恰当的是(    )

    核心考点: 略 

    2.(本小题14分) 已知：如图，BM平分∠ABC，P为BM上一点，PD⊥BC于点D，BD=AB+CD．
    求证：∠BAP+∠BCP=180°．

    （截长法）证明：如图，在BC上截取BE=BA，连接PE．

                               
    在△ABP和△EBP中

    ∴△ABP≌△EBP（SAS）
    ∴                           
                               
    ∴CD=ED
    ∵PD⊥BC
    ∴∠PDC=∠PDE=90°
    在△PCD和△PED中

    ∴△PCD≌△PED（SAS）
                               
    请你仔细观察下列序号所代表的内容：
    ①
    ；
    ②∵∠1=∠2；
    ③∠A=∠BEP；
    ④AP=PE；
    ⑤
    ；
    ⑥
    ；
    ⑦
    ；
    ⑧
    ．
    以上空缺处依次所填最恰当的是(    )

      核心考点: 略 

      3.(本小题14分) 已知：如图，BM平分∠ABC，点P为BM上一点，PD⊥BC于点D，BD=AB+DC．
      求证：∠BAP+∠BCP=180°．

      （补短法）证明：如图，                           

                                 
      ∵BP平分∠ABC
      ∴∠1=∠2
      在△BEP和△BDP中

      ∴△BEP≌△BDP（SAS）
                                 
      在△PEA和△PDC中

      ∴△PEA≌△PDC（SAS）
      ∴∠C=∠PAE
      ∵∠BAP+∠PAE=180°
      ∴∠BAP+∠BCP=180°
      请你仔细观察下列序号所代表的内容：
      ①延长BA，过点P作PE⊥BA于点E；
      ②延长BA到E，使AE=DC，连接PE；
      ③延长BA到E，使DC=AE；
      ④
      ；
      ⑤
      ；
      ⑥
      ；
      ⑦
      ．
      以上空缺处依次所填最恰当的是(    )

        核心考点: 略 

        4.(本小题14分) 已知：如图，在五边形ABCDE中，AB=AE，DA平分∠CDE，∠BAE=2∠CAD，求证：BC+DE=CD．

        （截长法）证明：如图，                        

        ∵DA平分∠CDE
        ∴∠1=∠2
        在△AFD和△AED中

        ∴△AFD≌△AED（SAS）
        ∴                        
                                
        在△ABC和△AFC中

        ∴△ABC≌△AFC（SAS）
        ∴BC=CF
        ∴BC+DE=CF+DF
        =CD
        请你仔细观察下列序号所代表的内容：
        ①在CD上截取CF=CB，连接AF；
        ②在DC上截取DF=DE，连接AF；
        ③在DC上截取DF=DE；
        ④AE=AF；
        ⑤AF=AE，∠4=∠3；
        ⑥∠4=∠3；
        ⑦
        ；
        ⑧
        ；
        ⑨
        ．
        以上空缺处依次所填最恰当的是(    )

          核心考点: 略 

          5.(本小题14分) 已知：如图，在五边形ABCDE中，AB=AE，∠BAE=2∠CAD，∠ABC+∠AED=180°，求证：BC+DE=CD．

          （补短法）证明：如图，                        

                                  
          在△ABC和△AEF中

          ∴△ABC≌△AEF（SAS）
          ∴∠2=∠3，AC=AF
                                  
          在△CAD和△FAD中

          ∴△CAD≌△FAD（SAS）
                                  
          请你仔细观察下列序号所代表的内容：
          ①延长DE到F，使EF=BC，连接AF；
          ②延长DE到F，使BC=EF；
          ③延长DE到F，连接AF；
          ④
          ；
          ⑤；
          ⑥
          ；
          ⑦
          ；
          ⑧
          ；
          ⑨
          ．
          以上空缺处依次所填最恰当的是(    )

            核心考点: 略 

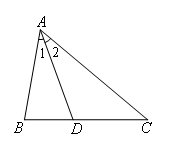
            6.(本小题14分) 已知：如图，在四边形ABCD中，AB=AD，∠D=∠ABC=∠BAD=90°，点E在CB的延长线上，点F在DC的延长线上，EAF=45°，连接EF．
            求证：DF=BE+EF．

            先在图上走通思路后再填写空格内容：
            ①要证明DF=BE+EF，是线段的和差倍分，考虑         ，解决本题用的是     ；
            ②结合条件∠D=∠ABC=90°，考虑                     （辅助线），然后证全等，理由是       ，由全等的性质得         ，为接下来的全等准备条件；
            ③由已证的全等和条件∠BAD=90°，EAF=45°，得        ，然后证全等，理由是       ，由全等的性质得         ，从而得DF=BE+EF．
            以上空缺处依次所填最恰当的是(    )

              核心考点: 略 

              7.(本小题16分) 已知：如图，在四边形ABCD中，AB=AD，E，F分别是DC，BC上的点，且满足，∠D+∠ABC=180°．
              求证：EF=BF+DE．

              先在图上走通思路后再填写空格内容：
              ①要证明EF=BF+DE，是线段的和差倍分，考虑         ，解决本题用的是     ；
              ②结合条件∠D+∠ABC=180°，考虑                     （辅助线），然后证全等，理由是       ；
              ③由已证的全等和条件，得        ，然后证全等，理由是       ，由全等的性质得         ，从而得EF=BF+DE．
              以上空缺处依次所填最恰当的是(    )

                核心考点: 略
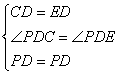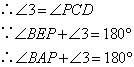
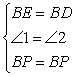
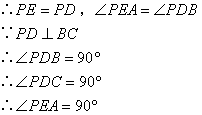