如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),
B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(0,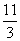),且将多边形OABCDE分割成
面积相等的两部分,则下列各点在直线l上的是(    )

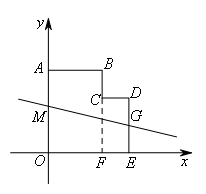
如图，延长BC交x轴于点F，设直线l交ED于点G
由题意可知：OA＝6，AB＝4，CD＝2，DE＝4
S_{多边形OABCDE}＝S_{四边形OABF}+S_{四边形CDEF}＝6×4+2×4＝32
∵直线l经过点M（0，），设直线l的表达式为：
当x＝6时，y＝，即G点坐标为（6，）
∴GE＝
∵多边形OABCDE被直线l分割成面积相等的两部分
∴S_{四边形OMGE}＝S_{多边形OABCDE}＝16
即：＝16
∴k＝
∴直线l的函数表达式是：
当x=4时，y=，则A不正确；
当x=5时，y=2，则B正确；
当x=6时，y=，则C不正确；
当x=2时，y=3，则D不正确；
故选B．

略