-
【2013-05-10 (
周五)】
如图，在△ABC中，
ABC=90°，AB=6，BC=8，动点P从点A出发，沿AC向点C移动．同时，动点Q从点C出发，沿CB向点B移动．在运动过程中，始终满足AP=2CQ，当其中有一点到达终点时，它们都停止移动．设CQ=x．
（1）求△CPQ的面积S关于x的函数解析式；
（2）在P，Q移动的过程中，当△CPQ为等腰三角形时，求出x的值．
先试着自己做一做再看答案哦~~
ABC=90°，AB=6，BC=8，动点P从点A出发，沿AC向点C移动．同时，动点Q从点C出发，沿CB向点B移动．在运动过程中，始终满足AP=2CQ，当其中有一点到达终点时，它们都停止移动．设CQ=x．
-
【2013-05-09 (
周四)】
如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB1∥AC．动点D从点A出发沿射线AC方向运动，同时动点E从点C出发沿射线AC方向运动．过点D作DH⊥AB于点H，过点E作EF⊥AC，交射线BB1于点F，G是EF的中点，连接DG．设AD=5a，CE=3a．
（1）当a为何值时，AD=AB，并求出此时DE的长；
（2）当△DEG与△ACB相似时，求a的值．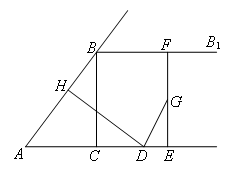
先试着自己做一做再看答案哦~~
-
【2013-05-08 (
周三)】
如图，矩形OABC在平面直角坐标系中，若OA=2，OC=
．
（1）求B，C两点的坐标；
（2）把△ABC沿AC对折，点B落在点B′处，线段AB′与x轴交于点D，求
直线BB′的解析式；
（3）在直线BB′上是否存在点P，使△ADP为直角三角形？若存在，请求出
点P的坐标；若不存在，请说明理由．
先试着自己做一做再看答案哦~~
．
-
【2013-05-07 (周二
)】
如图，在Rt△ABC中，ACB=90°，AC=6，BC=8，点D在边AB上运动，DE平分CDB交边BC于点E，EM⊥BD，垂足为M，EN⊥CD，垂足为N．
（1）当AD=CD时，求证：DE∥AC．
（2）探究：是否存在这样的AD，使得△BME与△CNE相似？
先试着自己做一做再看答案哦~~
-
【2013-05-06 (周一
)】
如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿着AB向点B运动；同时点Q从点C出发，沿CA向点A运动，当点P到达点B时，点Q随之停止运动．已知
．
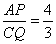（1）当AP为何值时，PQ∥BC？
（2）△APQ与△CQB能否相似？若能，求出AP的长；若不能，说明理由．
先试着自己做一做再看答案哦~~
．
