-
【2012-12-21 (
周五)】
如图,在平面直角坐标系中,O为坐标原点,Rt△OAB的直角边OA在x轴的正半轴上,点B坐标为(
 ,1),以OB所在直线为对称轴将△OAB作轴对称变换得△OCB.现有动点P从点O出发,沿线段OA向点A运动,动点Q从点C出发,沿线段CO向点O运动,两点同时出发,速度都为每秒1个单位长度.设运动时间为t秒.
,1),以OB所在直线为对称轴将△OAB作轴对称变换得△OCB.现有动点P从点O出发,沿线段OA向点A运动,动点Q从点C出发,沿线段CO向点O运动,两点同时出发,速度都为每秒1个单位长度.设运动时间为t秒.
(1)求∠AOC的度数;
(2)若四边形BCQP的面积为S(平方单位),求S与t之间的函数关系式;
(3)设PQ与OB交于点M,当△OMQ为等腰三角形时,求t的值.先试着自己做一做再看答案哦~~
-
【2012-12-20 (
周四)】
如图,在直角坐标系中,O是坐标原点,A,B,C三点的坐标分别为A(18,0),B(18,8),C(6,8),四边形OABC是梯形,点P,Q同时从原点出发,分别做匀速运动,其中点P沿OA向终点A运动,速度为每秒2个单位,点Q沿路线O→C→B运动,速度为每秒3个单位,当一点到达终点则另一点也停止运动,设运动的时间为t秒.

(1)求直线OC的解析式;
(2)从运动开始,梯形被直线PQ分割后的图形中是否存在平行四边形,若存在,求出t的值,若不存在,请说明理由;
(3)当t为何值时,直线PQ把梯形OCBA分成面积为1:7的两部分?先试着自己做一做再看答案哦~~
-
【2012-12-19 (
周三)】
如图,在直角坐标系中,点O是坐标原点,四边形OABC是平行四边形,点A的坐标为(14,0),点B的坐标为(18,
 ).
).
(1)求点C的坐标和平行四边形OABC的对称中心的点的坐标;
(2)动点P从点O出发,沿OA方向以每秒1个单位的速度向终点A匀速运动,动点Q从点A出发,沿AB方向以每秒2个单位的速度向终点B匀速运动,两点同时出发,当一点到达终点时另一点停止运动.设点P运动的时间为t秒(t>0),求当t为何值时,△PQC的面积是平行四边形OABC的一半?
(3)当△PQC的面积是平行四边形OABC面积的一半时,在平面直角坐标系中找到一点M,使以C,P,Q,M为顶点的四边形为平行四边形,请直接写出点M的坐标.

先试着自己做一做再看答案哦~~
-
【2012-12-18 (周二
)】
直线
 与坐标轴分别交于A,B两点,动点P,Q从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
与坐标轴分别交于A,B两点,动点P,Q从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
(1)直接写出A,B两点的坐标;
(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;
(3)当S= 时,求出点P的坐标,并直接写出以点O,P,Q为顶点的平行四边形的第四个顶点M的坐标.
时,求出点P的坐标,并直接写出以点O,P,Q为顶点的平行四边形的第四个顶点M的坐标.
先试着自己做一做再看答案哦~~
-
【2012-12-17 (周一
)】
已知:如图,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系,A,B,C三点的坐标分别为A(8,0),B(8,10),C(0,4),点D为线段BC的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OAB的路线移动,移动的时间为t秒.
(1)求直线BC的解析式;
(2)若动点P在线段OA上移动,当t为何值时,四边形OPDC的面积是梯形COAB面积的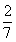 ?
?
(3)动点P从点O出发,沿折线OAB的路线移动过程中,设△OPD的面积为S,请直接写出S与t的函数关系式,并指出自变量t的取值范围.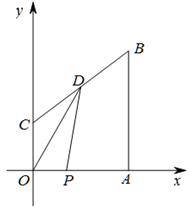
 (备用图)
(备用图)
先试着自己做一做再看答案哦~~









 (备用图)
(备用图)